コラム「SAS/JMPとの歩み」
第5回:SASとJMPで一生の研究を完成
-2012年末に全ての判別関数の問題が解決-
成蹊大学 経済学部教授
新村秀一
16.3重要な発見と改良(2000~2005年)[61-72]
アヤメのデータはFisherの仮説を満たすデータである.CPDデータは多重共線性のあるデータである.さらに特徴のある判別データを探したが良いものが見つからないので,SAS,JMPの入門の解説書に用いていた「学生(の合否判定)データ」を分析することにした.このデータは研究には適していないと思っていたが,一般位置にないデータでありIP-OLDF(と判別分析)のとんでもない瑕疵が分かった.最後に選んだスイス銀行紙幣データは,ドイツの統計学者Fluryらが集め判別分析の解説書にも用いているが,誰も2変数でMNM=0になることを発見できなかったが,IP-OLDFでそれが分かった.私は従来の統計的判別関数は「MNM=0のデータを認識できないばかりか,変数選択法に問題があり,判別分析の鬼門である」と確信するようになった.
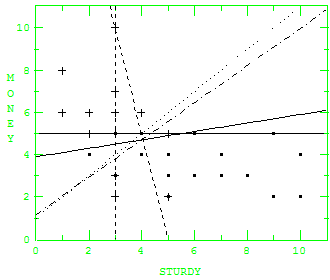
図4 各種判別超平面
(1)学生のデータ
図4は「学生データ」の勉強時間をX軸に支出をY軸にとった散布図である.成績が70点以上の25名を合格(・)とし,65点以下の15名を不合格(+)とした.X=3の垂直線に10人,Y=5の水平線に合格群と不合格群の各4名の学生がいる.例えばY=5 を判別超平面に選ぶと,Y<5 に21名の残りの合格群と3名の不合格群,Y>5に8名の不合格群がいる.これが「判別スコアがf(x)=0になるケースをどちらに判別してよいかは未解決の問題」の説明に適している.y>5で8名の不合格者が正しく判別され,Y<5の3名が誤判別される.また21名の合格者も正しく判別されるが,Y=5上の8名をどちらに判別するかは決定不能である.図に書き込んだ直線はほぼ45度の一点鎖線のLDFを含む各種線形判別関数の判別超平面である.右あがりの実線の改定IP-OLDF(M=30)は,X=5と6の間を通り,Y=5上にある2人を誤判別し,Y<5の3人の不合格者と合わせて5名が誤判別されてMNM=5になる.漫然とY≧5を不合格群あるいはY≦5を合格群としても4名が誤判別され,7名が最終的に誤判別される.判別分析にとってまさに鬼門のデータであり,新しい判別手法を開発した場合,検証に利用することを勧めます.
(2) スイス銀行紙幣データによる教師データの評価
-線形分離可能なデータの問題点-
本データは,スイス1000フラン紙幣の真札と偽札各100枚の6個の計測値データである.散布図でみると容易に2変数で判別できることが分かるが,なぜ誰もMNM=0にきずかなかったか不思議である.変数増加法とAICは5変数,Cp統計量は6変数のモデルを選ぶが,2変数(X4,X6)でMNM=0であり,MNMの単調減少性からこれらの2変数を含む16個のすべてのモデルが0になる.このデータを用いた判別分析の解説書が1988年に出版されて以来,著者のFluryや読者のだれもが気づかなかったことが示すように,従来の線形判別関数は「線形分離可能なデータを認識できないばかりか,判別分析の研究者もその困難さを理解していない」ことが分かる.
この研究の過程で,MNM=0のデータを容易に作ることを思いついた.アイリスデータやCPDデータといったMNM=0でない2群の平均値間の距離を拡大することでMNM=0のデータに作り替えることができる.しかし,各種変数選択法の検定統計量は元のデータと同じ判別モデルを選ぶことが分かった.すなわち,変数選択法はMNM=0か否かを考慮していないことになる.
16.4改定IP-OLDFとSVMとの比較(2006~2008年)[72-80]
改定IP-OLDFの開発で,数理計画法で多くの才能ある研究者を引き付けているSVMとの比較を考えた.ハードマージン最大化SVMは,線形分離可能な判別問題に対して,パターン認識で研究されてきたマージン概念を用い2つのサポートベクタ(SV)を考える.この2つの超平面で,データ空間は群1のみを含む領域,どちらも含まない領域,群2のみを含む領域に分ける. そしてこの2つのSV間の距離(マージン)2/∥w∥を最大化する基準を取り入れた判別を,マージン最大化SVMと呼んでいる.ただし,w=(a1,a2,…,ap)である.この基準は非線形最適化になるので,これと等価な次の最小化基準に変えることで,式(3)の2次計画法に変換できる.
MIN=∥w∥2/2=(a12+a22+…+ap2) /2; ・・・・・(3)
yi * g(xi)> 1 ; i=1,…,n
しかし,現実の問題は線形分離可能なことは少ないので,SVの反対側に幾つかのケースがくること許す式(4)のソフトマージン最大化SVM(S-SVM)が提案された.多くの才能ある研究者がこれを見て何も思わないのが不思議である.数理計画法という最適化手法使いながら,重みcの決め方が恣意的である.またSVMの研究者は,不思議なことにMNM=0のデータの判別を取り上げていない.
MIN=(a12+…+ap2) /2+c*Σei ; (4)
yi * g(xi)> 1-ei ; i=1,…,n
16.5100重交差検証法(2009~2010年)[81-84]
(1)評価データの作成
評価データに関しては,3種類のデータを作った.Type1は4種の実データから平均ベクトルと分散共分散行列を求め,数理システム㈱のMONACOという乱数生成ソフトで,実データと同じ分散共分散をもつ正規乱数を作製した.そして実データを教師データとして作成した判別関数をあてはめたところ,評価データの方が判別結果の良いものが出てきた.これはすぐに理由が分かった.実データから得た分散共分散行列を母集団と考えると,乱数は忠実にそのコピーであり,実データは正規性から乖離しているためである.
そして漸く実データから一様乱数で復元抽出しType2の2万件の標本を作ることにした[75].そして改定IP-OLDFと,MNMの近似解を求める改定IPLP-OLDFで時間測定を行った.最大CPDデータで100倍速いことが分かった.そこで,実データとケース数の同じ100組の標本を作製(Type3)し,100重交差検証法を行うことにした.LDFとロジスティック回帰の100重交差検証法のプログラムはJMP事業部の支援を得た.改定IPLP-OLDFは自分で作成した.両方のプログラムは[50]に掲載してある.これらの評価データの作成方法は大標本でない実データで検証したいユーザーの実証研究に役に立つので利用してほしい.
(2)100重交差検証法(Type3)
4種類の実データから一様乱数を用いて復元抽出し,100組の標本をリサンプリングした.説明変数の異なる135個の判別モデルに関して,教師データと評価データで100重交差検証法を行った.LDFとロジスティック回帰はJMPのスクリプトで,改定IPLP-OLDFは数理計画法ソフトのLINGOを用いた[11].実際には13,500個の3種類の判別関数を検討し,100組の誤分類数から135組の平均誤分類確率を求め比較を行った.MNM基準の有効性を次の点で実証できた.
表3は,2012年度に改定IPLP-OLDFの代わりに改定IP-OLDFとS-SVMを追加して見直したものである.LDFとロジスティック回帰とS-SVMの平均誤分類確率から,改定IP-OLDFのそれを引いたものの範囲を最小値と最大値で示す.最小値が正であれば,その値だけ改訂IP-OLDFの平均誤分類確率が小さいことを意味する.括弧の数字は,負になるモデル数を示す.LDFは,教師データのすべてで改定IP-OLDFより悪かった.評価データでは,アイリスデータ,銀行データ,学生データの6個のモデルで改定IP-OLDFより良いだけである.ロジスティック回帰は,教師データで2組,評価データで9組だけ改定IP-OLDFより良い.S-SVMは教師データで3組,評価データで18組良いだけである.
この研究成果は私自身にも驚きで良すぎた結果であった.教師データでMNMは全ての線形判別関数の誤分類数の下限値を与える.その代わり評価データの検証結果は確率分布を想定したLDFなどより悪くなると一般的に考えられた.しかしこの結果が分かれば,多くのデータは正規分布しないのに正規分布と仮定して求めたLDFは,評価データで良いことを期待するのが間違いであることが分かる.ロジスティック回帰が医学や経済で使われているのは,実務家はデータに合わせたロジスティック曲線で判別する方が良いことを知っているためである.
結局,MNM基準は評価データで誤分類確率をOverestimateしないことが分かった.
| LDF-改定IP | Logi-改定IP | SVM-改定IP | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 教師 | 評価 | 教師 | 評価 | 教師 | 評価 | |||||||
| 最小 | 最大 | 最小 | 最大 | 最小 | 最大 | 最小 | 最大 | 最小 | 最大 | 最小 | 最大 | |
| Iris(15) | 0.91 | 12.94 | -0.01(1) | 5.56 | 0.7 | 10.1 | 0.41 | 8.2 | 0.91 | 12.94 | -0.01(1) | 5.56 |
| 銀行(16) | 0.51 | 0.98 | -1.33(2) | 1.03 | 0 | 0 | -1.34(2) | 0.68 | 0.61 | 1.49 | -1.06(1) | 1.37 |
| 学生(31) | 1.18 | 8.61 | -1.61(3) | 6.77 | -2.42(2) | 6.63 | -3.13(7) | 5.56 | -0.6(1) | 15.4 | -5.62(12) | 2.22 |
| CPD(19) | 3.09 | 7.31 | 1.91 | 6.05 | 0.12 | 2.90 | 0.01 | 1.63 | -0.86(2) | 2.57 | -0.43(4) | 1.68 |
表3:LDFとロジスティック回帰の平均誤分類確率と改定IPLP-OLDFとの差の検討
これで一応基礎研究は終わり,統計的判別関数はMNM=0のデータを認識できないことを「試験の合否判定」で行う応用研究を2010年から取り組むことにした.大筋では思い通りの結果であるが,QDFが合格群の全てを誤判別するという驚く事実に直面し,3年間もがき苦しんだ.2012年11月の日本計算機統計学会で,分からないのであきらめるという人生で初めての敗北宣言を出した.しかし1週間後に急に分散共分散行列に基づく判別分析の問題であることに気づいて,2012年末に最後の問題が解決できた.そして,2013年から研究の見直しを行っていて,本コラムで紹介できないがさらに新しい知見も分かっている.
16.6応用研究(2010~2013年)[85-89]
| 2010 | 2011 | 2012 | ||
|---|---|---|---|---|
| 中間 | 0% | 31 | 25 | 21 |
| 10% | 48 | 42 | 37 | |
| 50% | 66 | 61 | 63 | |
| 90% | 82 | 79 | 78 | |
| 100% | 93 | 88 | 88 | |
| 平均 | 65.1 | 56.1 | 58.8 | |
| 期末 | 0% | 22 | 26 | 20 |
| 10% | 40 | 43 | 41 | |
| 50% | 60 | 60 | 58 | |
| 90% | 82 | 81 | 81 | |
| 100% | 91 | 99 | 95 | |
| 平均 | 59.3 | 57.1 | 58.8 | |
| r | 0.54 | 0.7 | 0.51 | |
| R2 | 0.29 | 0.49 | 0.26 |
表1 講義内容の比較
応用研究として,既存の統計的判別関数はMNM=0のデータを認識できず,変数選択に問題があることに絞ることにした.MNM=0のデータは,探しても簡単に見つかるものではない.しかし,「試験の合否判定」は身近で手に入る良質な研究データであることに気付いた.そこで,2010年から始めた成蹊大学経済学部の1年生に実施した「統計入門」の中間試験と期末試験の10択100問のマークセンス試験の合否判定を,得点分布の10%点,50%点,90%点で行うことにした.
(1)試験の概要
2010年度から成蹊大学経済学部の1年次生に開講した統計入門(必修)も3年になる.授業の質の評価と学生の達成度を調べる目的で,10択100問の中間と期末試験を行っている.試験の内容は数値を変えるだけで授業で行った内容を全て出題している.100問の設問を大学入試センター試験にならい4個の大問に分類し,得点分布の10%点,50%点,90%点の3水準で検討する.10%点は実際の合否判定基準であり,50%点は判別超平面近辺に多くの学生がくる試験,90%点は弁護士試験のような難易度の高い試験を想定している.
2010年度は手探りの状態であった.2011年度は授業の5週目から電力不足の問題で半舷授業になった.中間試験の範囲は1回削減し,期末試験の範囲は4回に削減した.2012年は過去2年間の試験結果を見直し,間違いやすい点の説明の改善を行ったので,3年間で連続して成績が向上することを期待した.しかし中間試験以降欠席者が増大したため,中間と期末試験では成績の入れ替わりが激しかった.しかし良くしたもので,中間に比べて期末の中央値以上は悪くない.中間試験の範囲は「基本統計量」,期末試験は「散布図と相関,単回帰,分割表と独立性の検定」と範囲が広いことを考えれば,中間試験は1年生にとって単に未知との遭遇で難しいが,期末は統計を面白いことが分かり出席率の高い学生にとって難しくなく中央値を押し下げていないと考えられる.数学が不得意な学生が多くて統計の授業がやりにくいというよりも,統計が役に立つ学問であるとアピールしモチベーションを高める必要がある.
(2)大問の合否判定
表4は,大問4問の得点を説明変数とした3水準の判別結果である.「p」列は,変数増加法で合否判定できた説明変数の個数を示す.MNMとLogiは,大問の4問から2問で合否判定できた.LDFとQDFは,大問4問使っても全試験で合否判定できなかった.18個の判別で,LDFの誤分類確率は[2.3,16.7],QDFは[0.8,10.8]になり合否判定できないことが分かる.中間試験の10%で合否判定を行うと,2010年度は大問4問で,2011年は3問で,2012年度は2問で合否判定ができ,2011年は「正規分布に関する設問」が,2012年はこれに加えて「基礎統計量の概念」が合否判定に不要であった.これは出題者として納得できる結果であり,他の結果もおおむね大問と合否水準の関係が分かり,試験の質保証に利用できる.例えば今年のセンター試験の国語は小林秀雄の大問が平均点を押し下げて話題になった.改定IP-OLDFで合否判定を行えば,多分10%や50%で合否判定に不要で,90%では変数増加法で最初に選ばれる可能性が高い.万が一90%でも合否判定に必要なければ,受験生のどの水準の合否判定にも役立たないことが分かる.
| 10% | 50% | 90% | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| P | MNM | Logi | LDF | QD | P | MNM | Logi | LDF | QD | P | MNM | Logi | LDF | QD | ||
| 中間 | 2010 | 4 | 0 | 0 | 9 | 2 | 4 | 0 | 0 | 3 | 6 | 3 | 0 | 0 | 20 | 10 |
| 2011 | 3 | 0 | 0 | 9 | 10 | 4 | 0 | 0 | 3 | 3 | 3 | 0 | 0 | 13 | 5 | |
| 2012 | 2 | 0 | 0 | 1 | 1 | 4 | 0 | 0 | 7 | 5 | 4 | 0 | 0 | 10 | 3 | |
| 期末 | 2010 | 4 | 0 | 0 | 5 | 2 | 4 | 0 | 0 | 4 | 5 | 4 | 0 | 0 | 4 | 13 |
| 2011 | 4 | 0 | 0 | 16 | 4 | 4 | 0 | 0 | 4 | 5 | 4 | 0 | 0 | 5 | 12 | |
| 2012 | 4 | 0 | 0 | 9 | 3 | 4 | 0 | 0 | 3 | 3 | 4 | 0 | 0 | 4 | 1 | |
(3)分散共分散行列による判別関数の問題
2群がFisherの仮説を満たせば,分散比最大化基準によるLDFが,容易に2群を表す正規分布N(m1,s1)とN(m2,s2)の対数尤度比で式(5)のように定式化される.
LDF:f(x)={x-(m1+m2)/2}’∑-1(m1-m2)・・・(5)
2群の分散共分散行列が等しくない場合,式(6)で2次判別関数(QDF)が定式化される.
f(x)=x’(∑2-1- ∑1-1) x/2+(m1’∑1-1-m2∑2-1)x+c ・・・(6)
また式(7)のマハラノビスの汎距離は,多群判別や品質管理のMT理論に応用されている.
D=SQRT ((x-m)’ ∑-1(x-m))・・・(7)
これに対して,分散比最大化基準は式(8)の数理計画法の最小化モデルで定式化できる.最初は制約式なしの非線形計画法で,次は分母を定数に置き換えて制約に取り込むことで2次計画法で解ける.この基準は判別関数を定式化しないでbを数理計画法で求めることができる.
MIN=b’(xm1-xm2) (xm1-xm2)’b/b’Sb;
あるいはMIN=b’(xm1-xm2) (xm1-xm2)’b;b’Sb=1;
m1とm2はclass1と2の平均,Sはプールした分散共分散行列・・・(8)
明らかに分散共分散行列の逆行列だけで定式化する式(5)の方が,統計ソフトとして実現しやすく,理論展開しやすいことは一目瞭然である.このため統計研究者であっても,単に2群が正規分布であると仮定して判別分析が発展してきたことに気づかず,あたかも重回帰分析と同列の推測統計学的手法であると誤解する向きもある.推測統計学的知見が得られないため,今日では役目を終えたleave one out法で学習データと検証データによる評価が必要であった.また,Fisherの仮説を満たさないデータにLDFを適用してはいけないという研究者もいたが,多次元正規性の検定法が確立していないので,LDFは使ってはいけないと言っていることと等しい.
大問の合否判定では,1)統計的判別関数が線形分離可能なデータを認識できないことが分かった.小問では分散共分散行列を用いた判別関数は,2)計測値がばらつかない場合に問題を起こすことを示す.スイス銀行紙幣データのようなMNM=0のデータを見つけることは困難である.しかし試験の合否判定を,設問の正解得点を説明変数と考えれば自明な線形分離可能な判別関数が求まる.すなわち良質なMNM=0のデータが容易に手に入る.これに対して合否判定を判別分析してもそれを将来別の試験に適用できないという指摘もあるが,入試やセンター試験の大問では出題するジャンルは決まっている.少なくとも大問で,合否判定に必要な設問と不要な設問を学習データで継続的に検討すれば,試験の質保証に役立つ.
(4)小問の合否判定
表5は,小問100個を説明変数とした合否判定である.各年度の上段は最初にMNM=0になった次元で,下段はフルモデルの誤分類数である.100問であるが,全員正解のため2010年では96変数がフルモデルになる.Logiは多くの場合MNM=0の場合に0になったが,90%の3個でできなかった.LDFとQDFは合否判定できなかった.フルモデルではLDFは合否判定でき,QDFは10%点では2010年の中間と2011年の期末以外の4個,50%点では2010年の期末の1個,90%点では5個の合否判定で,合格群がすべて不合格群に誤判別されるという異常状態になった.
| 年度 | P | MNM | Logi | LDF | QD | P | MNM | Logi | LDF | QD | P | MNM | Logi | LDF | QD | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 中間 | 2010 | 6 | 0 | 0 | 2 | 1 | 12 | 0 | 0 | 2 | 4 | 13 | 0 | 1 | 4 | 13 |
| 96 | 0 | 0 | 0 | 109 | 96 | 0 | 0 | 0 | 61 | 96 | 0 | 0 | 0 | 13 | ||
| 2011 | 12 | 0 | 0 | 2 | 107 | 15 | 0 | 0 | 3 | 6 | 9 | 0 | 0 | 6 | 9 | |
| 98 | 0 | 0 | 0 | 107 | 98 | 0 | 0 | 0 | 61 | 98 | 0 | 0 | 0 | 9 | ||
| 2012 | 6 | 0 | 0 | 7 | 114 | 19 | 0 | 0 | 1 | 3 | 15 | 0 | 1 | 1 | 12 | |
| 100 | 0 | 0 | 0 | 114 | 100 | 0 | 0 | 0 | 67 | 100 | 0 | 0 | 0 | 12 | ||
| 期末 | 2010 | 12 | 0 | 0 | 5 | 111 | 32 | 0 | 0 | 1 | 62 | 11 | 0 | 1 | 6 | 13 |
| 99 | 0 | 0 | 0 | 111 | 99 | 0 | 0 | 0 | 62 | 99 | 0 | 0 | 4 | 13 | ||
| 2011 | 8 | 0 | 0 | 4 | 4 | 13 | 0 | 0 | 6 | 7 | 8 | 0 | 0 | 2 | 12 | |
| 97 | 0 | 0 | 0 | 110 | 97 | 0 | 0 | 0 | 62 | 97 | 0 | 0 | 0 | 12 | ||
| 2012 | 10 | 0 | 0 | 3 | 115 | 10 | 0 | 0 | 5 | 4 | 9 | 0 | 0 | 6 | 12 | |
| 97 | 0 | 0 | 0 | 115 | 97 | 0 | 0 | 0 | 63 | 97 | 0 | 0 | 0 | 12 |
表5 小門の合否判定
試験の合否判定を大問4問で行い合格最低点を50点とすれば,F=T1+T2+T3+T4-49.5で,f>0なら合格,f<0なら不合格という自明な線形判別関数が求まる.
| p | VAR | MNM | pLDF | pQDF | 修正 | VAR | MNM | pLDF | pQDF |
|---|---|---|---|---|---|---|---|---|---|
| 1 | x85 | 10 | 14 | 14 | 14 | x92 | 12 | 12 | 12 |
| 2 | x15 | 6 | 14 | 114 | 28 | x42 | 8 | 8 | 12 |
| 3 | x68 | 5 | 8 | 114 | 28 | x21 | 5 | 5 | 12 |
| 4 | x47 | 3 | 8 | 114 | 28 | x54 | 4 | 8 | 12 |
| 5 | x7 | 1 | 4 | 114 | 9 | x65 | 1 | 3 | 12 |
| 6 | x32 | 0 | 5 | 114 | 3 | x100 | 1 | 3 | 12 |
| 7 | x20 | 0 | 3 | 114 | 0 | x83 | 1 | 3 | 12 |
表6 2010年の中間試験の10%と90%の合否判定
表6は2012年の10%と90%の変数選択法の結果である.10%では,設問85のあと設問15(不合格群の全員が不正解で,合格群がばらつく)で合格群の114名が不合格群に誤判別される.90%点では設問92で合格群の全員が正解であり不合格群に誤判別される.式(5)に見るようにLDFは2群のある説明変数が一定の場合,分散共分散行列はランク落ちする.QDFはこれに加えて,各2群の説明変数がバラツイテいないとランク落ちする.しかしJMPでは2群の分散共分散行列の対角要素を修正し,外れ値のあるダーティなデータにも対応している.それでも駄目な場合は正則化法を勧めこれまで上手くいってきた.しかし,今回の事例を想定して対応していなかったようで驚く結果になった.これ自体,「群に属するデータはバラツクもの」という統計的な思い込みの結果であろう.
| LDF | QDF | 平均の差 | |
|---|---|---|---|
| 2群の値が同じ | 省く | 省く | 省く |
| 2群が 別の一定値 | 省く | 省く | 省く |
| 一方が同じで, 他方がばらつく | 計算 | 誤判別 | 計算 |
| SPSS | 省く | 省く | 省く |
表7 判別で考慮すべき点
表7はこの問題を整理している.2群のある計測値の値が全て等しい場合は,LDF,QDF,平均の差の検定はこの変数を正しく省いている.2群のある計測値が別々の一定値の場合,この変数だけで判別でき判別に重要であるが省いている.この場合はこの変数は判別に役立つ旨をメッセージで出力すべきであろう.今回のように一方の計測値が一定で,他方がばらつく場合,LDFも平均の差の検定も判別に重要として計算するがQDFは誤判別する.この解消は簡単で,X15に平均0で分散が10‐9のような小さな乱数を加えるだけで,誤分類数は表6の修正欄のように14->28->28->28->9->3->0と7変数で合否判定できる.しかし90%点ではX92で合格群の12名が全て正解で不合格群がバラツクが,乱数を加えても結果は変わらない.すなわち,QDFは合否判定できない.多くの統計ソフトは全ての場合で,分散共分散行列はランク落ちするので,これらの変数を省いているが,利用者はこのことに留意して判別に役立つか否かを別途検討する必要がある.
17.大学教員としての棚卸
大学教員になることで,自分の生涯の研究テーマである「判別分析」の闇を退官前に解決した.しかし,多くの人にこの事実を知らせることはできていない.医学診断などは,判別超平面上に異常群に属する患者さんが一番多くくる試験のデータと同じ構造をもっている.品質管理やパターン認識でも同じことが言える.LDFやQDFで誤分類確率が例えば0.3であってもMNM=0であることを否定できない.またゲノム判別で,少ないケース数から多くの説明変数を用いた分散共分散行列の推定が行われているが,その信頼性に対して懸念する.
本コラムで少なくともSASユーザーへその一端を知らせることができたのは幸いである.もっと広く知らせる方法は,現在のところ解決の糸口を見つけていないので妙案があれば教えていただきたい.
文献
[61-65]新村秀一(2002).数理計画法を用いた最適線形判別関数(1)から(5).オペレーションズ・リサーチ47/1から47/5.
[66]_(2002).数理計画法を用いた最適線形判別関数(5)-決定木分析との比較-.成蹊大学経済学部論集,32-2,299-314.
[67]_(2002).数理計画法を用いた最適線形判別関数(6)-アルゴリズムの改善―.成蹊大学経済学部論集,33-1,93-114.
[68]_(2003).数理計画法を用いた最適線形判別関数(7)-計算機速度の劇的な改善.成蹊大学経済学部論集,33-2,183-188.
[69]_(2004).数理計画法を用いた最適線形判別関数(8)―524,287個の回帰モデルの検討―.成蹊大学経済学部論集,34-2,53-70.
[70]_(2004).数理計画法を用いた最適線形判別関数(9)―1000スイスフラン偽札紙幣の分析―.成蹊大学経済学部論集,35-1, 87-112.
[71]_(2004).数理計画法を用いた最適線形判別関数(10)―多重共線性の検討―.成蹊大学経済学部論集,35-2, 19-38.
[72]_(2005).OLDFとSVMの比較研究(1)-スイス銀行紙幣データと同じ構造をもつ2万件の正規乱数データによる検証-.成蹊大学経済学部論集,36-1,63-92.
[73]_(2006a).改定IP-OLDFによるSVMのアルゴリズム研究,オペレーションズ・リサーチ,51/11, 702-707.
[74]_(2006b).OLDFとSVMの比較研究(2)-改定IP-OLDFと改定LP-OLDFの提案-.成蹊大学経済学部論集,36-2,13-34.
[75]_(2007).OLDFとSVMの比較研究(3)-高速な組み合わせ最適化アルゴリズムの提案―.成蹊大学経済学部論集, 37-1,127-144.
[76]_(2007).数理計画法による判別分析の10年.計算機統計学, 20-1/2, 53-94.
[77]_(2007).改定IP-OLDFによるIP-OLDFの問題点の解消.計算機統計学, 19-1,1-16.
[78]_(2007).OLDFとSVMの比較研究(4)-種々のデータによるSVMとの比較-(共著).成蹊大学経済学部論集. 37-2,89-119.
[79]_(2008).OLDFとSVMの比較研究(6)-LINGOによる改訂IP-OLDFと改訂IPLP-OLDFの比較―.成蹊大学経済学部論集.38-2,35-56.
[80]_(2008).OLDFとSVMの比較研究(7)-IP-OLDFによる線形判別関数の新しいモデル選択法の提案―.成蹊大学経済学部論集.39-1,35-56.
[81]_(2009).線形計画法による改訂IP-OLDFの計算時間の改善.計算機統計学 22-1, 1-22.
[82]_(2008).OLDFとSVMの比較研究(8)-改訂IP-OLDFのリサンプリングデータによる評価―.成蹊大学経済学部論集,39-2,53-78.
[83]_(2009).OLDFとSVMの比較研究(9)-2万件リサンプリングデータによる10重交差検証法―.成蹊大学経済学部論集,40-1,21-72.
[84]_(2009).OLDFとSVMの比較研究(10)―k重交差検証法による新しい変数選択法―.成蹊大学経済学部論集,40-2,67-119.
[85]_(2010).Fisherの判別分析を越えて.成蹊大学経済学部論集,41-1,31-59 .
[86]_(2010).OLDFとSVMの比較研究(11)―ソフトマージン最大化SVMの考察―.成蹊大学経済学部論集,41-2,31-59.
[87]_(2011).最適線形判別関数の応用(2)-2011年度の統計入門の分析.成蹊大学経済学部論集,42-2,1-38.
[88]_(2012).最適線形判別関数の応用(3)-2010年度から2012年の統計入門の総括-.成蹊大学経済学部論集,43-2,1-32.
[89]_(2013).統計教育における判別分析の改善点.統計数理研究所共同研究レポート293-統計教育実践研究第5巻‐,36-45.