UNIVARIATEプロシジャ
- 概要
-
入門ガイド

-
構文

-
詳細
 欠損値 丸め 記述統計量 モードの計算 パーセント点の計算 位置の検定 正規分布のパラメータに対する信頼限界 ロバスト推定量 ラインプリンタプロットの作成 高解像度グラフの作成 CLASSステートメントを使用した比較プロットの作成 インセットの配置 当てはめた連続分布の計算式 適合度検定 核密度推定 Q-Qプロットと確率プロットの作成 Q-Qプロットと確率プロットの解釈 確率プロットとQ-Qプロットの分布 Q-Qプロットを使用した形状パラメータの推定 Q-Qプロットを使用した位置パラメータと尺度パラメータの推定 Q-Qプロットを使用したパーセント点の推定 入力データセット OUTPUTステートメントのOUT=出力データセット OUTHISTOGRAM=出力データセット OUTKERNEL=出力データセット OUTTABLE=出力データセット 要約統計量のテーブル ODSテーブル名 当てはめた分布のODSテーブル ODS Graphics 計算リソース
欠損値 丸め 記述統計量 モードの計算 パーセント点の計算 位置の検定 正規分布のパラメータに対する信頼限界 ロバスト推定量 ラインプリンタプロットの作成 高解像度グラフの作成 CLASSステートメントを使用した比較プロットの作成 インセットの配置 当てはめた連続分布の計算式 適合度検定 核密度推定 Q-Qプロットと確率プロットの作成 Q-Qプロットと確率プロットの解釈 確率プロットとQ-Qプロットの分布 Q-Qプロットを使用した形状パラメータの推定 Q-Qプロットを使用した位置パラメータと尺度パラメータの推定 Q-Qプロットを使用したパーセント点の推定 入力データセット OUTPUTステートメントのOUT=出力データセット OUTHISTOGRAM=出力データセット OUTKERNEL=出力データセット OUTTABLE=出力データセット 要約統計量のテーブル ODSテーブル名 当てはめた分布のODSテーブル ODS Graphics 計算リソース -
例
 複数の変数に対する記述統計量の計算 モードの計算 極値のオブザベーションと極値の表示 度数表の作成 ラインプリンタ出力プロットの作成 FREQ変数を使用したデータセットの分析 OUT=出力データセットへの要約統計量の保存 出力データセットへのパーセント点の保存 平均、標準偏差、分散に対する信頼限界の計算 分位点とパーセント点に対する信頼限界の計算 ロバスト推定の計算 位置の検定 対応のあるデータを使用した符号検定の実行 ヒストグラムの作成 一元比較ヒストグラムの作成 二元比較ヒストグラムの作成 記述統計量を含むインセットの追加 ヒストグラムのビン幅の指定 正規曲線をヒストグラムに追加する 当てはめた正規曲線を比較ヒストグラムに追加する ベータ曲線の当てはめ 対数正規曲線、Weibull曲線、ガンマ曲線の当てはめ 核密度推定の計算 3パラメータ対数正規曲線の当てはめ 折り重ねられた正規曲線の追加表示 対数正規確率プロットの作成 対数正規分布の当てはめを表示するヒストグラムの作成 正規確率プロットの作成 分布の参照線の追加 正規確率プロットの解釈 対数正規確率プロットから3パラメータを推定する 対数正規確率プロットからパーセント点を推定する 対数正規確率プロットからパラメータを推定する Weibull分布の分位点プロットの比較 累積分布プロットの作成 P-Pプロットの作成
複数の変数に対する記述統計量の計算 モードの計算 極値のオブザベーションと極値の表示 度数表の作成 ラインプリンタ出力プロットの作成 FREQ変数を使用したデータセットの分析 OUT=出力データセットへの要約統計量の保存 出力データセットへのパーセント点の保存 平均、標準偏差、分散に対する信頼限界の計算 分位点とパーセント点に対する信頼限界の計算 ロバスト推定の計算 位置の検定 対応のあるデータを使用した符号検定の実行 ヒストグラムの作成 一元比較ヒストグラムの作成 二元比較ヒストグラムの作成 記述統計量を含むインセットの追加 ヒストグラムのビン幅の指定 正規曲線をヒストグラムに追加する 当てはめた正規曲線を比較ヒストグラムに追加する ベータ曲線の当てはめ 対数正規曲線、Weibull曲線、ガンマ曲線の当てはめ 核密度推定の計算 3パラメータ対数正規曲線の当てはめ 折り重ねられた正規曲線の追加表示 対数正規確率プロットの作成 対数正規分布の当てはめを表示するヒストグラムの作成 正規確率プロットの作成 分布の参照線の追加 正規確率プロットの解釈 対数正規確率プロットから3パラメータを推定する 対数正規確率プロットからパーセント点を推定する 対数正規確率プロットからパラメータを推定する Weibull分布の分位点プロットの比較 累積分布プロットの作成 P-Pプロットの作成 - リファレンス
| 適合度検定 |
PROC UNIVARIATEステートメントでNORMALオプションを指定した場合や、HISTOGRAMステートメントで当てはめたパラメトリックな分布を要求した場合、分析変数の値が指定した理論分布からの無作為抽出であるという帰無仮説の適合度検定が計算されます。例4.22を参照してください。
NORMALオプションを指定した場合、これらの検定は"Tests for Normality"というラベルの出力テーブルに要約され、次の検定が含まれます。
Shapiro-Wilk検定
Kolmogorov-Smirnov検定
Anderson-Darling検定
Cramér-von Mises検定
Kolmogorov-Smirnov 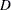 統計量、Anderson-Darling統計量およびCramér-von Mises統計量は、経験分布関数(EDF)に基づきます。ただし、指定した分布で特定の組み合わせのパラメータを推定する場合に、EDF検定がサポートされないことがあります。使用できるEDF検定の一覧は、表4.114を参照してください。帰無仮説を棄却するかどうかは、適合度検定に関連付けられている
統計量、Anderson-Darling統計量およびCramér-von Mises統計量は、経験分布関数(EDF)に基づきます。ただし、指定した分布で特定の組み合わせのパラメータを推定する場合に、EDF検定がサポートされないことがあります。使用できるEDF検定の一覧は、表4.114を参照してください。帰無仮説を棄却するかどうかは、適合度検定に関連付けられている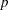 値を調べることにより判断できます。
値を調べることにより判断できます。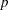 値が事前に定義された基準値(
値が事前に定義された基準値( )より小さい場合は、帰無仮説を棄却し、指定した分布からのデータではなかったと判断します。
)より小さい場合は、帰無仮説を棄却し、指定した分布からのデータではなかったと判断します。
分散分析法の正規性の仮定を検定する場合は、正規性の統計的検定を単独で使用するよう注意します。帰無仮説を棄却する検定力(検定の検出力)は、標本サイズに応じて高くなります。標本サイズが大きくなるほど、正規性からの小さな乖離を検出できます。正規性からの小さな偏差は分散性の分析検定の妥当性にはそれほど大きく影響しないため、他の統計量やプロットを調査して正規性の最終評価を行うことが重要です。歪度および尖度の測定値と、PLOTSオプション、HISTOGRAMステートメント、PROBPLOTステートメント、QQPLOTステートメントで得られるプロットが大変役立ちます。標本サイズが小さい場合、重要な正規性からの大きな乖離の検出力が低い場合があります。このような偏差の検定力を高くするには、よく使用される0.05の有意水準ではなく、0.15や0.20などの高い有意水準を使用する必要がある場合があります。この場合も、プロットや他の統計量を調べると、正規性からの偏差の大きさの評価に役立ちます。
Shapiro-Wilk統計量
標本サイズが2000以下の場合にNORMALオプションを指定すると、PROC UNIVARIATEはShapiro-Wilk統計量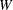 (標本サイズ
(標本サイズ に依存することを強調するために
に依存することを強調するために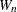 とも表記されます)を計算します。
とも表記されます)を計算します。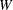 統計量は、分散の通常の修正平方和推定量に対する、(順序統計量の線形結合の2乗に基づく)分散の最良推定量の比率です(ShapiroおよびWilk; 1965)。
統計量は、分散の通常の修正平方和推定量に対する、(順序統計量の線形結合の2乗に基づく)分散の最良推定量の比率です(ShapiroおよびWilk; 1965)。 が3より大きい場合、順序統計量の線形結合を計算するための係数は、Royston (1992)法により近似されます。統計量
が3より大きい場合、順序統計量の線形結合を計算するための係数は、Royston (1992)法により近似されます。統計量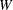 は、常に0より大きく1以下です
は、常に0より大きく1以下です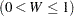 。
。
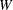 の値が小さい場合、正規性の帰無仮説は棄却されます。
の値が小さい場合、正規性の帰無仮説は棄却されます。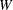 は片寄りの大きい分布です。一見すると大きい
は片寄りの大きい分布です。一見すると大きい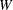 の値(0.90など)が小さいと見なされ、帰無仮説の棄却が導き出される場合があります。
の値(0.90など)が小さいと見なされ、帰無仮説の棄却が導き出される場合があります。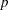 値(観測値以下の
値(観測値以下の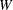 統計量を取得する確率)の計算方法は
統計量を取得する確率)の計算方法は に依存します。
に依存します。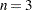 の場合、
の場合、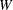 の確率分布は既知で、
の確率分布は既知で、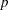 値の決定に使用されます。
値の決定に使用されます。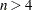 の場合、正規化変換は次のように計算されます。
の場合、正規化変換は次のように計算されます。
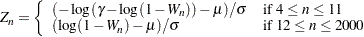 |
 、
、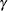 および
および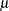 の値は、シミュレーション結果から得られる
の値は、シミュレーション結果から得られる の関数です。
の関数です。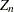 の値が大きい場合は正規性から乖離していることを示し、統計量
の値が大きい場合は正規性から乖離していることを示し、統計量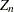 はほぼ標準正規分布であることから、この分布を使用して
はほぼ標準正規分布であることから、この分布を使用して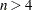 の場合の
の場合の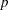 値が決定されます。
値が決定されます。
EDF適合度検定
パラメトリックな分布を当てはめた場合、PROC UNIVARIATEは経験分布関数(EDF)に基づく一連の適合度検定を出力します。EDF検定は検出力が高く、ヒストグラムの中間点によって検定結果が変わらないなどの点で従来的なカイ2乗検定より優れています。詳細は、D’Agostino and Stephens (1986)を参照してください。
経験分布関数は、 個の独立するオブザベーション
個の独立するオブザベーション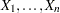 に対し、一般的な分布関数
に対し、一般的な分布関数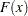 で適宜されます。オブザベーションは、
で適宜されます。オブザベーションは、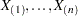 のように昇順に表記します。経験分布関数
のように昇順に表記します。経験分布関数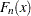 は次のように定義されます。
は次のように定義されます。
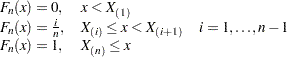 |
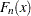 は、オブザベーションごとに高さ
は、オブザベーションごとに高さ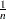 のステップを取る関数です。この関数は分布関数
のステップを取る関数です。この関数は分布関数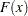 を推定します。任意の値
を推定します。任意の値 で、
で、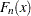 は
は 以下の比率で、
以下の比率で、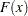 は
は 以下のオブザベーションの確率です。EDF統計量は、
以下のオブザベーションの確率です。EDF統計量は、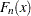 と
と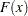 の間のディスクレパンシを測定します。
の間のディスクレパンシを測定します。
EDF統計量の計算式では、確率積分変換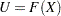 を利用します。
を利用します。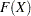 が
が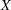 の分布関数である場合、乱数変数
の分布関数である場合、乱数変数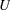 は0~1の間の均等な分布になります。
は0~1の間の均等な分布になります。
 個のオブザベーション
個のオブザベーション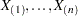 がある場合、値
がある場合、値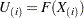 は、次の3つのセクションの説明にあるように、変換を適用して計算されます。
は、次の3つのセクションの説明にあるように、変換を適用して計算されます。
PROC UNIVARIATEでは、次の3つのEDF検定を行うことができます。
Kolmogorov-Smirnov
Anderson-Darling
Cramér-von Mises
次のセクションで、これらのEDF統計量の計算式の定義を示します。
KolmogorovのD統計量
Kolmogorov-Smirnov統計量(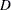 )は次のように定義されます。
)は次のように定義されます。
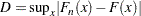 |
Kolmogorov-Smirnov統計量は、EDF統計量の上限値クラスに属します。この統計量のクラスは、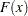 と
と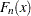 の垂直方向の最大差に基づきます。
の垂直方向の最大差に基づきます。
Kolmogorov-Smirnov統計量は、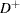 および
および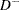 の最大値として計算されます。
の最大値として計算されます。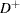 はEDFが分布関数より大きい場合のEDFと分布関数の間の最大垂直距離、
はEDFが分布関数より大きい場合のEDFと分布関数の間の最大垂直距離、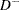 はEDFが分布関数より小さい場合の最大垂直距離です。
はEDFが分布関数より小さい場合の最大垂直距離です。
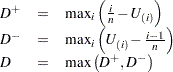 |
PROC UNIVARIATEでは、修正済みKolmogorov 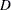 統計量を使用して、平均および分散が標本と等しい正規分布に対してデータを検定します。
統計量を使用して、平均および分散が標本と等しい正規分布に対してデータを検定します。
Anderson-Darling統計量
Anderson-Darling統計量およびCramér-von Mises統計量は、EDF統計量の2次クラスに属します。この統計量のクラスは、2乗差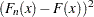 に基づきます。2次統計量の一般形は次のとおりです。
に基づきます。2次統計量の一般形は次のとおりです。
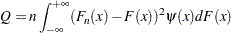 |
関数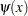 は2乗差
は2乗差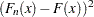 を重み付けします。
を重み付けします。
Anderson-Darling統計量(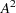 )は次のように定義されます。
)は次のように定義されます。
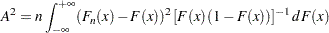 |
ここで、重み関数は 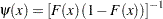 です。
です。
Anderson-Darling統計量は次のように計算されます。
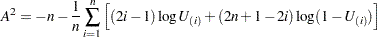 |
Cramér-von Mises統計量
Cramér-von Mises統計量(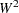 )は次のように定義されます。
)は次のように定義されます。
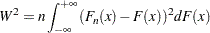 |
ここで、重み関数は 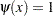 です。
です。
Cramér-von Mises統計量は次のように計算されます。
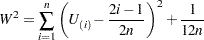 |
EDF検定の確率値
EDF検定統計量が計算されると、PROC UNIVARIATEは関連する確率値(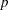 値)を計算します。
値)を計算します。
Gumbel、逆ガウス、一般化パレート、レイリー分布の場合、PROC UNIVARIATEは、推定した分布から再サンプリングすることによって、関連する確率値(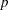 値)を計算します。デフォルトでは、500個のEDF検定統計量が計算され、指定した(当てはめた)分布のEDF検定統計量と比較されます。標本数は、EDFNSAMPLES=nの設定によって制御できます。たとえば、5000個のシミュレーションに基づく、Gumbel分布の適合度検定の
値)を計算します。デフォルトでは、500個のEDF検定統計量が計算され、指定した(当てはめた)分布のEDF検定統計量と比較されます。標本数は、EDFNSAMPLES=nの設定によって制御できます。たとえば、5000個のシミュレーションに基づく、Gumbel分布の適合度検定の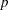 値を要求するには、次のステートメントを使用します。
値を要求するには、次のステートメントを使用します。
proc univariate data=test; histogram / gumbel(edfnsamples=5000); run;
ベータ、指数、ガンマ、対数正規、正規、べき関数、Weibull分布の場合、UNIVARIATEプロシジャは、D’AgostinoおよびStephens (1986)によって示されたものと似た確率水準の内部テーブルを使用します。値が2つの確率水準の間の場合、線形補間を使用して確率値が推定されます。
確率値は、既知のパラメータと分布に対して推定されたパラメータに依存します。表4.114は、さまざまな当てはめた組み合わせに対して、EDF検定を使用できるかどうかをまとめたものです。
分布 |
パラメータ |
使用可能な検定 |
||
|---|---|---|---|---|
いき値 |
尺度 |
形状 |
||
ベータ |
|
|
|
すべて |
|
|
|
すべて |
|
指数 |
|
|
すべて |
|
|
|
すべて |
||
|
|
すべて |
||
|
|
すべて |
||
ガンマ |
|
|
|
すべて |
|
|
|
すべて |
|
|
|
|
すべて |
|
|
|
|
すべて |
|
|
|
|
すべて |
|
|
|
|
すべて |
|
|
|
|
すべて |
|
|
|
|
すべて |
|
対数正規 |
|
|
|
すべて |
|
|
|
|
|
|
|
|
|
|
|
|
|
すべて |
|
|
|
|
すべて |
|
|
|
|
すべて |
|
|
|
|
すべて |
|
|
|
|
すべて |
|
正規 |
|
|
すべて |
|
|
|
|
||
|
|
|
||
|
|
すべて |
||
べき関数 |
|
|
|
すべて |
|
|
|
すべて |
|
Weibull |
|
|
|
すべて |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
すべて |
|
|
|
|
すべて |
|
|
|
|
すべて |
|
|
|
|
すべて |
|
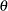 既知
既知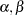 既知
既知 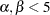 未知
未知  未知
未知 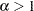 未知
未知 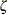 既知
既知  既知
既知 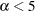 未知
未知  既知
既知  既知
既知 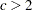 既知
既知 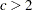 既知
既知