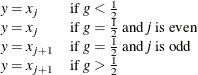UNIVARIATEプロシジャ
- 概要
-
入門ガイド

-
構文

-
詳細
 欠損値丸め記述統計量モードの計算パーセント点の計算位置の検定正規分布のパラメータに対する信頼限界ロバスト推定量ラインプリンタプロットの作成高解像度グラフの作成CLASSステートメントを使用した比較プロットの作成インセットの配置当てはめた連続分布の計算式適合度検定核密度推定Q-Qプロットと確率プロットの作成Q-Qプロットと確率プロットの解釈確率プロットとQ-Qプロットの分布Q-Qプロットを使用した形状パラメータの推定Q-Qプロットを使用した位置パラメータと尺度パラメータの推定Q-Qプロットを使用したパーセント点の推定入力データセットOUTPUTステートメントのOUT=出力データセットOUTHISTOGRAM=出力データセットOUTKERNEL=出力データセットOUTTABLE=出力データセット要約統計量のテーブルODSテーブル名当てはめた分布のODSテーブルODS Graphics計算リソース
欠損値丸め記述統計量モードの計算パーセント点の計算位置の検定正規分布のパラメータに対する信頼限界ロバスト推定量ラインプリンタプロットの作成高解像度グラフの作成CLASSステートメントを使用した比較プロットの作成インセットの配置当てはめた連続分布の計算式適合度検定核密度推定Q-Qプロットと確率プロットの作成Q-Qプロットと確率プロットの解釈確率プロットとQ-Qプロットの分布Q-Qプロットを使用した形状パラメータの推定Q-Qプロットを使用した位置パラメータと尺度パラメータの推定Q-Qプロットを使用したパーセント点の推定入力データセットOUTPUTステートメントのOUT=出力データセットOUTHISTOGRAM=出力データセットOUTKERNEL=出力データセットOUTTABLE=出力データセット要約統計量のテーブルODSテーブル名当てはめた分布のODSテーブルODS Graphics計算リソース -
例
 複数の変数に対する記述統計量の計算モードの計算極値オブザベーションと極値の表示度数表の作成基本要約プロットの作成FREQ変数を使用したデータセットの分析OUT=出力データセットへの要約統計量の保存出力データセットへのパーセント点の保存平均、標準偏差、分散に対する信頼限界の計算分位点とパーセント点に対する信頼限界の計算ロバスト推定の計算位置の検定ペアのデータを使用した符号検定の実行ヒストグラムの作成一元比較ヒストグラムの作成二元比較ヒストグラムの作成記述統計量を含むインセットの追加ヒストグラムのビン幅の指定正規曲線をヒストグラムに追加する当てはめた正規曲線を比較ヒストグラムに追加するベータ曲線の当てはめ対数正規曲線、Weibull曲線、ガンマ曲線の当てはめ核密度推定の計算3パラメータ対数正規曲線の当てはめ折り重ねられた正規曲線の追加表示対数正規確率プロットの作成対数正規分布の当てはめを表示するヒストグラムの作成正規分位点プロットの作成分布参照線の追加正規分位点プロットの解釈対数正規分位点プロットから3パラメータを推定する対数正規分位点プロットからパーセント点を推定する対数正規分位点プロットからパラメータを推定するWeibull分布の分位点プロットの比較累積分布プロットの作成P-Pプロットの作成
複数の変数に対する記述統計量の計算モードの計算極値オブザベーションと極値の表示度数表の作成基本要約プロットの作成FREQ変数を使用したデータセットの分析OUT=出力データセットへの要約統計量の保存出力データセットへのパーセント点の保存平均、標準偏差、分散に対する信頼限界の計算分位点とパーセント点に対する信頼限界の計算ロバスト推定の計算位置の検定ペアのデータを使用した符号検定の実行ヒストグラムの作成一元比較ヒストグラムの作成二元比較ヒストグラムの作成記述統計量を含むインセットの追加ヒストグラムのビン幅の指定正規曲線をヒストグラムに追加する当てはめた正規曲線を比較ヒストグラムに追加するベータ曲線の当てはめ対数正規曲線、Weibull曲線、ガンマ曲線の当てはめ核密度推定の計算3パラメータ対数正規曲線の当てはめ折り重ねられた正規曲線の追加表示対数正規確率プロットの作成対数正規分布の当てはめを表示するヒストグラムの作成正規分位点プロットの作成分布参照線の追加正規分位点プロットの解釈対数正規分位点プロットから3パラメータを推定する対数正規分位点プロットからパーセント点を推定する対数正規分位点プロットからパラメータを推定するWeibull分布の分位点プロットの比較累積分布プロットの作成P-Pプロットの作成 - リファレンス
UNIVARIATEプロシジャは、各分析変数の最小値および最大値と、1番目、5番目、10番目、25番目、50番目、75番目、90番目、95番目、99番目のパーセント点(分位点)を自動的に計算します。これらのデフォルトパーセント点以外のパーセント点を計算するには、OUTPUTステートメントのPCTLPTS=オプションおよびPCTLPRE=オプションを使用します。
PCTLDEF=オプションで、5つのパーセント点計算定義のうち1つを指定できます。nは変数の値が非欠損値であるオブザベーション数、![]() は並べ替えられた変数の値を表すとします。また、t番目のパーセント点がyであるとし、
は並べ替えられた変数の値を表すとします。また、t番目のパーセント点がyであるとし、![]() と設定した上で、次の式が成り立つとします。
と設定した上で、次の式が成り立つとします。
ここで、jはnpの整数部分、gはnpの小数部分です。この場合、PCTLDEF=オプションはt番目のパーセント点yを次の表に記述したように定義します。
|
PCTLDEF |
説明 |
公式 |
|---|---|---|
|
1 |
|
|
|
ここで、 |
||
|
2 |
npに最も近い番号のオブザベーション |
|
|
3 |
経験分布関数 |
|
|
4 |
重み付き平均 |
|
|
( |
ここで、 |
|
|
5 |
平均化された経験分布関数 |
|
WEIGHTステートメントを使用する場合、パーセント点は異なる方法で計算されます。100p番目の重み付きパーセント点yは、平均化された経験分布関数から計算されます。
![\[ y = \left\{ \begin{array}{cl} x_1 & \mbox{if} \ w_1 > pW \\ \frac{1}{2} ( x_ i + x_{i+1} ) & \mbox{if} \sum _{j=1}^{i} w_ j = pW \\ x_{i+1} & \mbox{if} \sum _{j=1}^{i} w_ j < pW < \sum _{j=1}^{i+1} w_ j \end{array} \right. \]](images/procstat_univariate0177.png)
ここで、![]() は
は![]() に関連付けられた重みであり、
に関連付けられた重みであり、![]() は重みの合計です。
は重みの合計です。
PCTLDEF=オプションは、WEIGHTステートメントが使用される場合は適用されません。ただし、この場合、重みがすべて同じであれば、重み付きパーセント点は、WEIGHTステートメントを使用せずにPCTLDEF=5で計算されるパーセント点と同じになります。
CIPCTLNORMALオプションを使用すると、データが正規分布であると仮定して、パーセント点の信頼限界を要求できます。
これらの限界については、Hahn and Meeker (1991)のセクション4.4.1で説明されています。![]() の場合、
の場合、![]() 番目のパーセント点の両側の
番目のパーセント点の両側の![]() 信頼限界は次のようになります。
信頼限界は次のようになります。
ここで、nは標本サイズです。![]() の場合、
の場合、![]() 番目のパーセント点の両側の
番目のパーセント点の両側の![]() 信頼限界は次のようになります。
信頼限界は次のようになります。
片側の![]() 信頼限界は、適切な前の式の
信頼限界は、適切な前の式の![]() を
を![]() に置き換えて計算されます。因子
に置き換えて計算されます。因子![]() は、非心t分布に関連し、Owen and Hua (1977)およびOdeh and Owen (1980)に説明されています。例4.10を参照してください。
は、非心t分布に関連し、Owen and Hua (1977)およびOdeh and Owen (1980)に説明されています。例4.10を参照してください。
CIPCTLDFオプションを使用すると、パーセント点の分布によらない信頼限界を要求できます。特に、データが正規分布であると仮定する必要がありません。これらの限界については、Hahn and Meeker (1991)のセクション5.2で説明されています。![]() 番目のパーセント点の両側の
番目のパーセント点の両側の![]() 信頼限界は次のようになります。
信頼限界は次のようになります。
ここで、![]() は、データ値が昇順で並べ替えられている場合のj番目の順序統計量であり、次の式が成り立ちます。
は、データ値が昇順で並べ替えられている場合のj番目の順序統計量であり、次の式が成り立ちます。
下のランクlと上のランクuは、![]() の前後で対称(またはほぼ対称)な整数です。ここで、
の前後で対称(またはほぼ対称)な整数です。ここで、![]() は
は![]() の整数部分であり、 nは標本サイズです。また、lとuは、次の包含確率要件を満たしながら、
の整数部分であり、 nは標本サイズです。また、lとuは、次の包含確率要件を満たしながら、![]() および
および![]() ができるだけ
ができるだけ![]() に近くなるように選択されます。
に近くなるように選択されます。
ここで、![]() 累積二項確率であり、次のように表されます。
累積二項確率であり、次のように表されます。
特にnが小さく、pが0または1に近似している場合、包含要件を満たせないことがあります。対称性の要件を緩和するため、CIPCTLDF(TYPE = ASYMMETRIC)を指定することができます。このオプションは、包含要件を満たすことができる場合は対称限界を要求し、それ以外の場合は非対称限界を要求します。
CIPCTLDF(TYPE = LOWER)を指定すると、片側の![]() 下位信頼限界が
下位信頼限界が![]() として計算されます。ここで、lは次の不等式を満たす最も大きい整数です。
として計算されます。ここで、lは次の不等式を満たす最も大きい整数です。
![]() も満たします。同様に、CIPCTLDF(TYPE = UPPER)を指定すると、片側の
も満たします。同様に、CIPCTLDF(TYPE = UPPER)を指定すると、片側の![]() 下位信頼限界が
下位信頼限界が![]() として計算されます。ここで、uは次の不等式を満たす最も大きい整数です。
として計算されます。ここで、uは次の不等式を満たす最も大きい整数です。
パーセント点の信頼限界は、WEIGHTステートメントが指定されている場合は計算されません。例4.10を参照してください。