CORRプロシジャ
サブセクション
Pearsonの積率相関は、2変数の連関性のパラメトリックな統計量です。これは、線形関係の強度と方向の両者を測定します。ある変数Xが別の変数Yの完全な線形関数である場合、相関が1ならば正の関係が存在し、相関が-1ならば負の関係が存在します。2変数間に線形の予測可能性が存在しない場合、相関は0になります。2変数が相関0で正規である場合、これらの2変数は独立です。ただし、因果関係が存在しない場合もあるため、相関は因果性を意味するものではありません。
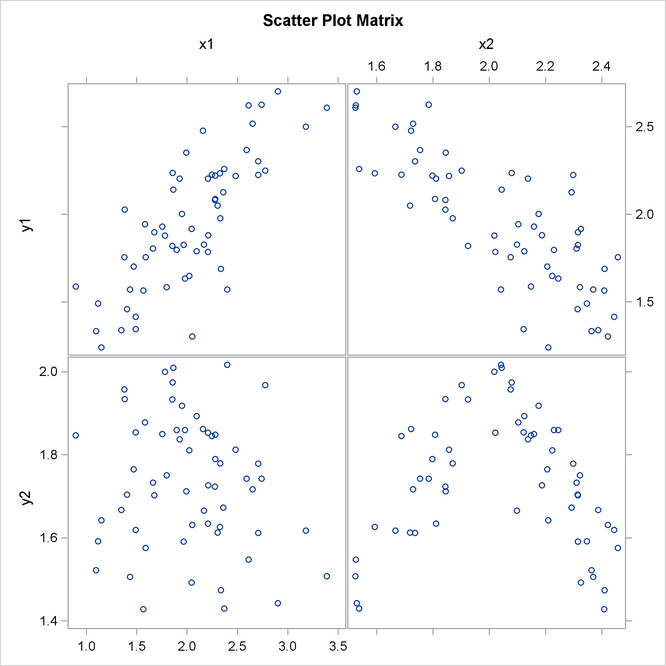
2つのランダムな数値変数間の関係を表示する散布図を図2.4に示します。
上記の散布図は、変数Y1とX1間には正の関係が存在し、変数Y1とX2間には負の関係が存在すること、および変数Y2とX1間には明確な相関が存在しないことを示しています。また、上記の散布図は、Y2がX2に従属しているにもかかわらず、変数Y2とX2間には明確な相関が存在しないことも示しています。
母集団Pearson積率相関
は次の式で表されます。
![\[ {\rho }_{xy}=\frac{\mr{Cov}(x,y)}{\sqrt {\mr{V}(x) \mr{V}(y)}} = \frac{\mr{E}(\, (x - \mr{E} (x)) (y - \mr{E} (y))\, )}{\sqrt {\mr{E}(x-\mr{E}(x))^{2}\, \mr{E}(y-\mr{E}(y))^{2}}} \]](images/procstat_corr0027.png){kind=small}
Pearson積率相関や重み付き積率相関などの標本相関は、母集団相関を推定します。標本Pearson積率相関は次の式で表されます。
![\[ r_{xy}=\frac{\sum _ i ( \, (x_ i-\bar{x})(y_ i-\bar{y})\, )}{\sqrt {\sum _{i}(x_ i-\bar{x})^{2} \, \sum _{i}(y_ i-\bar{y})^2}} \]](images/procstat_corr0028.png){kind=small}
ここで、
はxの標本平均、
はyの標本平均です。重み付きPearson積率相関は次の式で表されます。
![\[ r_{xy}=\frac{\sum _ i \, w_ i(x_ i-\bar{x}_ w)(y_ i-\bar{y}_ w)}{\sqrt {\sum _ i w_ i(x_ i-\bar{x}_ w)^2 \, \sum _ i w_ i(y_ i-\bar{y}_ w)^2}} \]](images/procstat_corr0031.png){kind=small}
ここで、 
は重み、 
はxの重み付き平均、 
はyの重み付き平均です。
![\[ t \, = \, {(n-2)}^{1/2} \, {\left(\frac{r^{2}}{1-r^{2}}\right)}^{1/2} \]](images/procstat_corr0035.png){kind=small}
