コラム「SAS/JMPとの歩み」
第4回:SASとJMPで一生の研究を完成
-学位取得まで-
成蹊大学 経済学部教授
新村秀一
15.判別分析の深い闇を切り開く
(1)判別分析の抱える問題
1936年にFisherは、p個の説明変数の線形結合f(x)=a0+a1X1+…+apXpから「2群の分散比最大化基準」でFisherの線形判別関数(LDF)の世界を切り開きました。その後さまざまな最適化基準で種々の判別関数が提案され、パターン認識、医学診断、経済の各種格付けや企業の倒産あるいは優良企業と不良企業の判別、最近ではゲノム判別へと応用されています。しかし判別分析は「f(x)>0なら群1、f(x)<0なら群2と判別するという単純な判別規則」に隠れて、大きな問題が未解決のまま放置されてきました。そして多くの統計家の中でも誤解と混乱を生んでいます。
1)f(x)=0のケースをどちらに判別するかは未解決です。統計ソフトでSASだけがこの問題を意識して、f(x)=0の扱いをユーザーが指定できます。一方JMPでは、ロジスティック回帰で2*2の分割表に判別結果をまとめる際、どの群を陽性と指定するかを問い、判別境界上のケースを全て陽性に判別しているようです。
2)「2群が多次元正規分布し分散共分散が等しいといういわゆるFisherの仮説」を置けば、多次元正規分布の対数尤度からFisherが導出したLDFと同じものが求まります。この定式化があまりに見事なため、この仮説を満たさないデータにLDFを適用してはいけないという異論を唱える人も多くいます。しかし、「2群の分散共分散行列が等しいという仮説を満たさない」場合は、2次判別関数(QDF)を先人は開発しました。このことは、先人はFisherの仮説を満たさないデータがあることを知っていたことを示します。また近年医学や経済分野でロジスティック回帰が用いられています。判別結果がLDFやQDFに比べて良いことが多いためですが、判別成績がよいのは「Fisherの仮説」を考えず、データに合わせてオッズ比の対数尤度を求めているからです[50] 。
3)判別境界を動かせば得られた判別結果より良いものが得られることが多くあります。結果があまりにも悪い場合には「正規性からの乖離」と言ってあきらめてきました。また判別境界を動かしてより良い判別結果を求める研究をしている若手研究者も多くいます。すでに述べたように、判別分析で事前確率やリスクを導入し判別境界を自由に動かす手法が既に与えられています。そこでそれを評価するためにROC曲線の利用を提案しました。
4)田口玄一先生は、正規分布に現れるマハラノビスの距離を用いて、正常状態の分散共分散行列から異常を考える1クラス判別分析を提案されています。私が考えた正常群と異常群の「地球モデル」と同じく、ある種の判別問題にFisherの2群判別の概念を持ち込む危うさを示しています。
以上の全ての点が、私が1998年から2010年まで行ってきた「最適線形判別関数[51]」の研究で解決しました。また新しく次の問題点が解決しました。詳しくは解説書[52]と論文などを参考にしてください。
5)筆者の研究で初めて分かったことですが、既存のLDF、QDF、ソフトマージン最大化SVMは、線形分離可能なデータを認識できないことです。また、変数選択法の統計量はMNM=0の最小次元を基準にして考えると一定の傾向を示しません。ロジスティック回帰は、回帰係数の推定が不安定になり誤分類数が0になれば、線形分離可能なデータを認識したことが筆者の開発した最適線形判別関数(改定IP-OLDF)から分かります。しかし、最小次元のMNM=0の空間を必ず求める保証はありません。ハードマージン最大化SVMは、線形分離可能なデータを識別できますが、MNM=0以外のデータに適用できない問題点があります。
6)判別関数の誤分類数と判別係数は推測統計学とは無縁であり、この関係が分かりませんでした。筆者の研究で、判別係数は定数項が正と0と負の3つの異なった構造をもち、MNMが最少な最適凸体の内点を判別係数とする最適線形判別関数を考えれば判別分析の抱える問題が解決できることが分かりました。
7)LDFやQDFは、試験の合否判定という自明な線形分離可能なデータを認識できず、LDFでは誤分類確率が0.34、QDFでは0.9以上になることが分かりました。
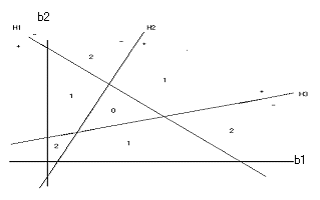
図1 判別係数の空間と誤分類数の関係
(2)2次元における3個のケースの判別例
最適線形判別関数の概略を、次の2個の説明変数をもつ3ケースで説明します。
群 1:x1 = (-1/18, -1/12),
群 2:x2 = (-1, 1/2),x3 = (1/9, -1/3)
さらに記号yiは群1の場合1とし,群2の場合-1とすることで、yi*f(x)>0であれば正しく判別され、yi*f(x)<0であれば誤判別されたとすることで不等号の向きを統一できます。
yi*f(x)=ax’+1, yi*gi(b)= xi b’+1
判別係数aとxは交換可能であり、xの値を係数とする次の3つの線形式を考えます。
H1 = y1*g1(b)
=- (1/18) × b1 - (1/12) × b2+1=0,
H2 = y2*g2(b)= -b1 + (1/2) × b2 + 1=0,
H3 = y3*g3(b)= (1/9) × b1 - (1/3) × b2 + 1 =0
これらの線形式は図1に示すとおり、判別係数を表す2次元平面b =(b1,b2)を7個の凸体に分割します。Hi上の点を判別係数bとすると、ケースxiが“判定保留群”に属し、その他のケースはyi*gi(b)>0であれば判別係数bを用いたyi*f(x)= b x’+1>0はxiを正しく判別し、yi*gi(b)<0であればxiを誤判別します。すなわち、各凸体の内点でyi* gi(b)<0になる図に書き込んだ数が誤分類数で、しかも内点を判別係数に用いれば判別超平面上にケースがくることを避けられます。そして、最小の誤分類数をもつ凸体を最適凸体と呼ぶことにすると、MNM基準による最適線形判別関数はこの最適凸体の内点に対応した判別関数になります。
定数項を1に固定して考えましたが、一般に正の実数cに固定すると、図1の各軸との切片はc倍になり、相似変換されただけで本質的な構造は変わりません。またこのcが0に収束していけば切片も0に収束し、3個の超平面は原点を通る第2の構造になります。またcが負であれば、正の場合と異なったc=-1と相似な構造になります。すなわち、判別係数と誤分類数は3つの異なった構造で説明できます。
(3)IP-OLDFと改定IP-OLDFと改定IPLP-OLDFの定式化
上の例題を一般化すると、次の整数計画法を用いたIP-OLDFになります。yiは群1の場合は1で群2の場合は-1、xiは説明変数のデータ、bは判別係数、eiはxiが正しく判別される場合は0に誤分類される場合は1に対応する1/0の整数値です。誤分類されるケースの制約式は、yi×(xi’b+1)>=0 からyi×(xi’b+1)>=-1に変わることで制約式が満たされます。目的関数はこのeiが1になる誤分類数の和を最小化します。ただしこのモデルはデータで表わされる配置行列が一般位置にある場合は最適凸体の頂点を正しく求めますが、一般位置にない場合は正しい最適凸体の頂点を求めないこともあることが分かりました。一方、eiを非負の実数にしたものをLP-OLDFといいます。数理計画法の判別分析研究で行われてきたL1ノルム判別分析の一種です[52]。ただし、誤分類されるケースの判別超平面上からの距離の和を最小化しても、現実的に意味がないのでこの種の研究成果は利用されてきませんでした。
MIN =Σei ;
yi×(xi’b+1)>=-ei ; i=1,…,n (1)
改定IP-OLDFは、パターン認識で古くから考えられているマージン概念を取り入れて式(2)のように定式化します。マージンの反対側にきて誤分類される全てのケースxiの制約式は、yi×(xi’b+1)>=1 からyi×(xi’b+1)>=-9999に変わりyi×(xi’b+1)=-9999というSVに引き寄せられます。これで判別超平面上にケースは含まれなくなるので、正しい最適凸体の内点が得られます。
MIN =Σei ;
yi×(xi’b+1)>=1-10000×ei ; (2)
改定LP-OLDFは、式(2)のeiを0/1の整数変数から非負の決定変数に変えただけです。
改定IP-OLDFは整数計画法を用いているので計算時間がかかります。そこで最初に改定LP-OLDFを適用し、ei =0になる正しく判別されたケースを第2段階で0に固定します。そして第1段階で1と誤判別されたものだけに改定IP-OLDFを適用することで、MNMの近似値が高速に求められます。これによって100重交差検証法の適用が可能になりました。
(4)MNMの有用性
1)MNMの単調減少性:p変数モデルのMNMをMNMpと表すことにします。このモデルに1変数追加した(p+1)変数モデルのMNM(p+1)は、必ず減少します(MNMp≧≧ MNM(p+1))。この証明は簡単です。追加した説明変数の判別係数を0とすれば、その(p+1) 変数モデルの誤分類数はMNMpになります。よって、(p+1)変数モデルのMNM(p+1)はMNMpより小さいか等しくなります。これで、変数増加法で選ばれるモデルのMNMも単調に減少することになります。
MNMの単調減少性から「線形分離可能な最小次元のデータ空間」の発見ができます。すなわち、MNMp≧=0であれば、このp変数を含む全ての判別モデルのMNMは0になります。
2)正規性からの乖離を示す尺度: データがFisherの仮説を満たせば、得られた誤分類数はMNMに等しくなります。すなわち、LDFの誤分類数がMNMから大きいほど、データが正規性からの乖離していることが分かります。
3)MNMによる判別手法の評価:MNMで他の判別手法の誤分類数を単回帰分析し評価できます。
16.人生をかけた研究
1996年に大学に移って良かったことの一つに、研究業績として評価が低いので嫌う研究者が多いですが、年2回経済学部論集が出され自分の論文を投稿できることがあります。大学に赴任した1996年以降ウイーン滞在の1回を除いて全ての号に寄稿しています。学会誌と異なり、査読者とのやり取りの時間が限りなく少ないので、タイムリーに成果を発表し、自分にとっても研究履歴が分かります。最適線形判別関数の研究は、空理空論でなく、多くの実証研究に裏付けられているので、タイムリーに記録を紀要に残せたことはありがたいことです。
16.1博士号の研究テーマの決定
日本医科大学の三宅章彦先生とは、Fisherの仮説を認めたうえで母集団と標本の誤分類確率に関する研究[41]を行いました。また誤分類数最小化(Minimum Number of Misclassifications, MNM)基準による最適線形判別関数を、ヒューリスティックなアプローチで行いました[53]。IBMの汎用機でアンダーテーブル研究として行ったため体系的な研究ができず、CPDデータを用いた6変数の分析結果だけです。また、SASで正規乱数を作って評価データとして分析しましたがそれほど良い結果ではありませんでした。そこで研究はそれ以上継続せず、終わりになりました。
1995年の秋に両国の住商情報システム(株)で私が大会長になり、日本計算機統計学会のシンポジュームを開きました。1996年には成蹊大学の教員になってからすぐに、岡山大学の垂水先生から「うちで学位をとりませんか」といわれていたが回答していませんでした。1997年9月に東北大学で行動計量学会がありました。夕食を食べに街に出ると、垂水先生にあって再度すすめられました。「大学に移って間もないので、岡山まで通うことはできないのですが?」というと「論文博士で考えています」ということで、数日考えて学位申請することにしました。研究テーマを夜考えていて、「数理計画法は関数の最大/最小値を求める学問である」から、誤分類数最小化基準による最適線形判別関数が定式化できないはずがないと思い考え始めると、すぐに定式化を思いつきました。すでにLinus教授のテキスト(実践数理計画法(朝倉、1992))の翻訳で回帰分析の数理計画法による定式化は知っていたので、それほどハードルは高くありませんでした。もし私が普通の研究者のように、既存の論文を探していたら1980年代から線形計画法を使ったL1ノルム基準による判別関数の論文が数多く出ていたので、整数計画法を用いた最適線形判別関数などの研究は行わなかったでしょう。実はその事実を知ったのは、2005年ごろLinus 教授から届いた先行研究の論文リストからです。
自分の人生の勉強のテーマの統計と数理計画法はソフトウエアを使って独学でマスターしていましたが、それらが連携していませんでした。日本では統計と数理計画法は数理工学科などで教えられていますが、同級生であっても専攻が違うと研究では永遠の平行線になります。それがこれでようやく自分の中でもつながることになりました。
16.2博士号取得まで(1998年~2000年3月)[54-60]
(1)FisherのアイリスデータとCPDデータによる実証研究
Fisherのアイリスデータは、FisherがLDFの検証に用いたため、こう呼ばれていますが、実際はEdgarが集めたデータです。 Fisherの仮説も誰が考えたのかわかりません。折につけ、「ご存知の方は教えてください」と言っていますがいまだに分かりません。そしてLDFをFisherの仮説を満たさないデータに適用してはいけないという方もいます。「判別したい2群が多次元正規分布か否かを示す良い統計量はないので、どう判定するのでしょうか。」このように本人の同意を得ないでFisherの名前を付けるのは、Fisherも望んでいないと思うがいかがでしょうか?本データは、相関係数を散布図で事前にチェックしないと間違った判断をするという統計入門の良い教材になります。IP-OLDFとLDFとQDFで、15個(=24-1)の判別モデルを分析し15個の誤分類数を評価しました。2群の分散共分散行列が等しくないときLDFに代わってQDFを用いることを判別理論で勧めていますが、その場合でもQDFの誤分類数が多いものが出てくるのでこのガイドラインは間違っていることが分かりました。
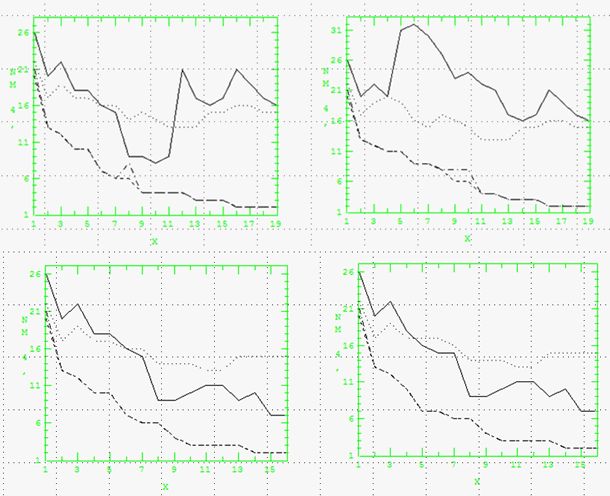
図2 CPDデータの誤分類数
(上左:19変数の増加法,上右:減少法,下左:16変数増加法,下右:16変数減少法)
CPDデータは17個の計測値と、2組の2変数の差で作られた2変数の計19変数あります。作成された2変数が判別に重要であることを示すことを目的としていますが、VIFで多重共線性があることが分かります。19変数と多重共線性を解消した16変数で変数増加法と変数減少法を行い40個の判別モデルに限定して考えます。この成果はSCSのIBM上ですでにSASのRSQUAREを使って分析していたものを再利用し、QDFとIP-OLDFとLP-OLDFの誤分類数を付け加えました。図2の上は、19変数のフルモデルに対して左は変数増加法、右は変数減少法の誤分類数をプロットしました。実線はQDFを表します。変数増加法では10変数まで誤分類数は減少し、それ以降増えるのは多重共線性に関係する変数がモデルに入ってくるからです。点線はLDFで、誤分類数が13以下に減らないことが分かります。証明したわけではありませんが変数選択法で選ばれた説明力のある有力な変数で作られた分散共分散である程度の構造が決まってしまうのではないかと考えています。これに対してIP-OLDFとLP-OLDFは8変数でLP-OLDFが悪くなっていますが、単調に減少しています。これからMNMの単調減少性という重要な事実が分かります。右の変数減少法では、QDFは6変数まで誤分類数が増加し、多重共線性に関係する変数が掃き出されると減少しています。それ以外は変数増加法とほぼ同じ傾向を示します。
図の下は、16変数のモデルの誤分類数のプロットで、QDFは多重共線性がなくなったのでどちらもほぼ減少傾向を示します。その他は19変数とほぼ同じ傾向です。以上からQDFは多重共線性に対して問題があることが分かります。このような大きな瑕疵をもつ手法は、利用すべきではないということです。
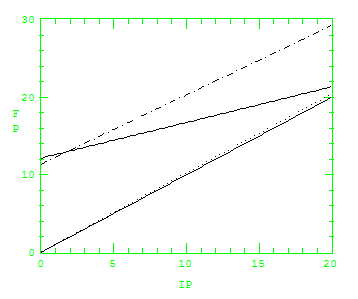
図3 各判別関数の誤分類数をMNMで単回帰
(QDF:1点鎖線、LDF:直線、LP-OLDF:点線、MNM;下の直線)
図3は、QDF (1点鎖線)、LDF (直線)、LP-OLDF(点線)、MNM(下の直線)の誤分類数を目的変数にしてMNMで単回帰したものです。X軸はMNMの値なので大きくなると説明変数が少ないことを表します。これによってQDFは一般的にMNMより12例(誤分類確率で0.05)悪くなります。LDFはフルモデルでは12例ほど悪いですが、説明変数が少なくなると2例まで少なくなります。
(2)2変量正規分布による教師データと評価データの検証
IP-OLDFとLP-OLDFに関する理論と、アヤメとCPDデータの実証研究を途中成果として垂水先生に送ったところ、乱数実験も付け加えるようコメントが来ました。統計研究では、乱数データによって研究内容の正当性を証明するのが常套手段です。しかし、「現実のデータはFisherの仮説を満たすものが少ない」という仮説にたって研究を進める予定であったので、種々の特徴のある実データで検証しようと考えていました。しかし、教師データ(内部標本)で判別関数を作成し、分析に用いていない評価データ(外部標本)で最終的に評価する必要があります。実データを教師データとして良い結果を得ましたが、評価データに関する見通しがありませんでした。そこでSpeakeasyという数学ソフトでXの標準偏差が2で、Yが1の2変量正規乱数を400個作成しました。最初の100件は群1の教師データ、次の100件を群1の評価データとし、次の200件を群2の教師データと評価データとしました。
そして群1の平均を原点に固定し、0度、30度、45度、60度、90度で回転した5組の標本を行列の積で作成しました。次に群2のXの値には0から8までの整数i、Yに0、2、4の整数jを加えて平行移動しました。これらの5*9*3個の組合せの教師と評価データを作成して、検証を行うことにしました。群1で回転を0度、群2でY=0に固定した8組の教師データと評価データのペアだけがFisherの仮説を満たします。それ以外はお互いの長軸が平行でないため、XとYの分散が異なり、Fisherの仮説の「2群の分散共分散が等しい」を満たさない状態を作ることができます。
教師データで各誤分類数をMNMで単回帰分析し「IP-OLDF<QDF<LDF< LP-OLDF」という傾向にあることが分かります。 評価データでは「QDF<IP-OLDF<LDF< LP-OLDF」という結果になり、QDFが一番良くなりました。わずか2変数の正規乱数であるため、LDFよりQDFの判別成績が良くなります。乱数を用いることで、頭の中で考えた分散共分散が異なる場合は、LDFに代わってQDFを用いるというガイドラインの正しいことが分かります。しかし、多重共線性にあるCPDデータの実証研究で、QDFには問題であることが分かったので、このガイドラインは利用しない方がよいことになります。
(3)学位取得
1999年秋に、田中豊先生を主査、垂水先生を副査とした論文審査が行われました。英語での1時間の発表を何とか乗り切りました。そして2000年3月に学位授与式に臨みました。1971年の大学卒業式以来でした。実は研究を始めた当初、100頁以上の英語の学位論文と、ドイツ語の筆記試験があると聞かされ、辞退しようかと思いました。数学科にはいったのは、Gaussにあこがれてゲッチンゲン大学に留学したいという漠然とした夢がありました。入学後、フランスのブルバキと呼ばれる数学者集団の書籍の影響か、フランス語を取りました。大学のドイツ語の先輩教員に速習法を聞きましたが、できの悪い学生のような質問に対して要領を得ませんでした。学位をとるために、ドイツ語の勉強に時間を割くつもりもありませんでした。しばらくして、今年から学位論文が英語であれば、第2外国語の筆記試験がなくなっていたと連絡があり、首一つで助かりました。実は学位取得後の研究で一番苦労したのは、現実に合った評価データを得ることでした。実は、2004年にウイーンでJMPの解説書のレビューをしていて乱数生成法が載っていて、もう少し早くJMPユーザーになっておればと思いました[24]。しかし苦しまぎれに、群1を回転させ、群2は平行移動させて135組の異なった2群の判別問題を作るアイデアは、自分としては気に入っています。読者も分析したいデータを用いて条件を変えて評価データを自由に作成すればよいと考えます。
また、2000年にヘルシンキで開催されたISIの後で、エストニアの古都のタルトの会議で発表しました。幸いに論文の投稿を勧められ10頁の論文が掲載されました[58]。幸先は良かったのですが、その後に外国語論文の投稿をしたところ、「信じられない」とか「分からない」というおよそ研究者のコメントとは思えない理由でリジェクトされることが多かったです。何も理論だけでなく、検証可能な実証研究も行っているのに中々理解されないことは、自分にとって残念に思います。すなわち、信じられない結果であれば自分で簡単に追試してみればすぐに分かることです。
文献
[24] 新村秀一(2004).(レビュー)JMPを用いた統計およびデータ分析入門.SAS Japan
[41] A.Miyake & S.Shinmura (1976). Error rate of linear discriminant function, F.T. de Dombal & F.Gremy , editors 435-445, North- Holland Publishing Company
[50] 新村秀一(2007 ).ExcelとLINGOで学ぶ数理計画法.丸善.
[51] 新村秀一(2010).最適線形判別関数.日科技連.
[52] 新村秀一(2011).数理計画法による問題解決法.日科技連.
[53] 三宅章彦,新村秀一(1980a).最適線形判別関数のアルゴリズムとその応用,医用電子と生体工学,18-1,15-20.
[54] 新村秀一(1998).数理計画法を用いた最適線形判別関数.計算機統計学.11-2,89-101.
[55] 新村秀一,垂水共之(1999).2変量正規乱数データによるIP-OLDFの評価.計算機統計学12-2,107-123.
[56] 新村秀一(2000).数理計画法を用いた最適線形判別関数(1).成蹊大学経済学部論集,30-2,193-215.
[57] 新村秀一(2000).最適線形判別関数(2)-アイリスデータへの適用-.成蹊大学経済学部論集,31-1,297-313.
[58] Shuichi Shinmura. (2000). A new algorithm of the linear discriminant function using integer programming. New Trends in Probability and Statistics 5,133-142.
[59] 新村秀一(2001).数理計画法を用いた最適線形判別関数(3)-多重共線性のある医学データの分析-.成蹊大学経済学部論集,31-2,207-236.
[60] 新村秀一(2001).数理計画法を用いた最適線形判別関数(4)-2変量正規乱数データによるIP-OLDFの評価―.成蹊大学経済学部論集,32-1,249-273.