随想「マーケティングとデータ解析」
第2回 統計学の独習記
朝野熙彦
中央大学客員教授
前号では「行き当たりばったり半生記」と題して、私と仕事との幸せな出会いを紹介させていただきました。私は良いデータ・アナリストが育つ条件は「よい本」「よい仲間」「よい仕事」の3つだと考えています。今回は私が若者時代に仕事をしながらどのように統計学の勉強をしたかを披露させていただきます。
INDEX
1.実社会への貢献
私が研究しているマーケティングは基礎学問ではなく実学ですので、マーケティングのためのデータ解析も実践活動そのものといえます。
データ解析を学ぶ上でよい本を読むことはもちろん大切ですが、マーケティングはただ本を読んで思索にふけるだけで済む学問ではないことはご承知ください。
書斎で読書しているだけではデータ解析の上手なユーザーにはなれないでしょう。データ解析の本当の教科書は本の中にも教室の黒板の上にもなく、データ解析が応用される実社会にあるのではないでしょうか。もしデータ解析をした結果が社会の現実と乖離がある場合は、データ解析の側が反省するという謙虚な姿勢が大事だと思います。
データ解析に取り掛る前に、データ自体がどのような環境と文脈(コンテクスト)の下で得られたのかを理解しておくことも大切です。そもそもデータ解析で用いる統計モデルが、分析したい現象のモデルとしては不適切であるかもしれません。モデルが不適切ならデータ解析がうまくいくはずがありません。私も自分自身の無知のためにそうした失敗を何度も経験してきました。
理論は理論として整合性がなければなりませんが、その理論が実社会で役立つかどうかは実社会が答えを出すことです。データ解析の価値は現実の世界にどれだけ貢献できたかによって評価すべきでしょう。故鳥井道夫氏(元サントリー名誉会長)が日本マーケティング協会会長の時代に述べられた「マーケティングとは売ってなんぼの実践学だ」という認識は、そのままデータ解析にも当てはまると思います。(鳥井道夫(1997)「大才中才小才」プレジデント社、16頁)
データ解析のおかげでビジネスを成功に導けたのかが問われるべきです。世の中には本当の意味で実践に貢献してきたデータ解析があります。医学や薬学がまさにそうです。また推測統計学の発祥となった農学そして推測統計学を社会に普及させることになった生産管理も、真摯にデータ解析の実践活動を積み重ねて産業界の発展に貢献してきたのです。
それらと比べるとマーケティングの実務の世界では、マーケティング提案を裏付けるための都合のよい道具、あるいは取引先企業を感心させるためのギミックとしてデータ解析を使うことはなかったでしょうか。先輩諸科学の研究姿勢を見習いたいと思います。
2.素晴らしい本との出会い
前号で自己紹介しましたように私は調査のイロハも知らないままマーケティング・リサーチの会社に入りましたので、入社後にゼロから勉強をしなければなりませんでした。マーケティング・リサーチの仕事で難しい問題が出てくると独りで、あるいは仲間とともにマーケティングや統計学、その他もろもろの勉強をしました。目標志向だといえば恰好はよいのですが、ありていに言えば「泥縄式」でした。会社員時代に数百件の新製品や新規事業の開発に携わりましたが、プロジェクトが始まる前から必要な知識がそろっていた、というような案件はめったになく、プロジェクトが始まってから付け焼刃で勉強を始めた場合がほとんどでした。
大学はその理想的な存在意義としては、
A:大学生の間に社会で役立つ勉強をしっかりと身に着ける
B:社会に出てから学生時代に身に着けた勉強を仕事に生かす
C:そうして大学が社会に貢献できることを実証してみせる
という幸せなストーリーを描いております。本当にA⇒B⇒Cの理想通りに実践できている学生もいないわけではありません。たまたま私個人のケースでは、
A’:大学生の間に社会で役立つ勉強を身に着けなかった
B’:社会に出てから仕事に必要な勉強を始めた
C’:そのため大学が社会に貢献できることは実証できなかった
というパスをたどっただけのことです。
私と一緒に勉強してくれる仲間は職場には少なかったですね。でもマーケティング・リサーチの仕事を通じてだんだんと社外の仲間が増えてきました。そもそも仕事を発注してくれたお客様が真っ先に仲間に加わってくれました。「よい仕事」と「よい仲間」が混然一体となってグループ学習をしたものです。その後、大学の教員になってゼミを担当するようになってからの話ですが、ゼミ生でグループを作って論文の講究をさせてみました。集団で講究した方が、学生の勉強意欲も持続できるし教育効果が上がるように思われました。もちろん独習が良いのか、それともグループ学習が良いのかは個人の性格にもよるでしょうから、一概にどちらが良いと押し付けるつもりはありません。
さて、若いころ私が読んだ懐かしい本に、竹内啓・柳井晴夫「多変量解析の基礎」東洋経済新報社(1972年)、という本がありました。
この本は線形空間への射影という大変すっきりした概念で多変量解析を解き明かした本です。各種の多変量解析は、それぞれの方法ごとに目的関数が設定できて、その最大化をはかると多くの場合、固有値・固有ベクトルを計算する問題に帰着することが知られていました。しかし、あれはあれ、これはこれの計算問題という感じで統一的な見通しに欠けていたのです。それに対して線形空間に別の線形空間を射影するという唯一のアイデアだけですべての多変量解析が一気に説明できるという透徹した原理は爽快でした。もちろん非線形の多変量解析については同じアイデアでは対応できませんが、1970年代のマーケティング界では非線形の分析はめったに使われていませんでした。この本がきっかけになって、当時若者だった私は統計解析に興味を持つようになったのです。全くの初心者ではありましたが、データ解析の面白さに目覚めてしまった瞬間です。
ですからこの本がその後の自分の人生を導いてくれた本であることは間違いありません。心から感謝できる本にめぐり合えたことは私の幸せでした。
ところでこの本の初版には数式展開や記号に関する誤植がたくさんありました。プライム(’)が抜けているだの+と-が逆だのといった些細な印刷ミスが100個所くらいはあったでしょう。ミスを訂正しながら精読することはとても楽しいものです。論理にあいまいさが無く明瞭に書かれた本だからこそ間違いにも気づくのです。著者は読者がミスを訂正しながら勉強できるように、親切心で校正モレを残しておいてくれたのかもしれません。(違うか)
なお、誤植について一般論を言わせていただくと、最先端の研究をされている学者は、常に新しい研究に没頭しているために、脱稿後の本の校正をしている余裕がないという事情があります。もう一つ「多変量解析の基礎」の場合は、この本の大部分を執筆された柳井先生の字が達筆すぎて、印刷所の人に判読しがたかったという事情があります。私の知る限りですが、優れた学者はとかく手書きでは読みづらい字を書かれる傾向にありました。そう、当時は原稿用紙のマス目に鉛筆や万年筆で原稿を書いていたものでした。
後日談ですが、柳井晴夫・竹内啓「射影行列・一般逆行列・特異値分解」東京大学出版会(1983年)、というこれも素晴らしい本がその後出版されました。相変わらず100個所どころではなく校正モレがありまして、そのことを柳井先生に伝えました。すると印刷ミスを書きこんだ本を貸してくれ、こんど増刷する時に参考にするから、という読者にとっては誠に光栄なご依頼を受けました。さすがに一流の研究者だけあって、沽券にかかわるなどと立腹しないものだと感心した次第です。
3.疑いつつ読めば勉強になる本
ただの印刷ミスの問題ではなくて論旨そのものが間違っている本も存在します。特に調査のための実務マニュアル本の中には統計学的な観点からみて間違いといってよい記述が少なくありません。ひとつ例題を出してみましょう。
【例題】平均値の95%信頼区間
母集団での平均値をμ、分散を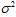 とする。母集団の規模をN、サンプルの大きさをnとする。
とする。母集団の規模をN、サンプルの大きさをnとする。
サンプルの平均値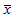 の分布はN-nとnが大きければ正規分布に近似する。
の分布はN-nとnが大きければ正規分布に近似する。
母集団から無作為抽出して標本平均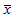 を求めると、
を求めると、
平均値の95%は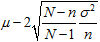 より大きく
より大きく
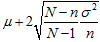 より小さい。
より小さい。
つまり信頼度95%で
 ……………………………① である。このことから
……………………………① である。このことから
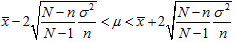 ………② が導ける。
………② が導ける。
通常Nは極めて大きいので、近似的に真の平均値μは信頼度95%で
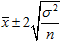 …………………………………………③ の範囲に入る。
…………………………………………③ の範囲に入る。
これを平均値のサンプリング誤差という。
母集団の分散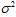 は未知なので、標本分散
は未知なので、標本分散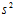 に置き換えて
に置き換えて
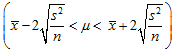 …………………④ を平均値の95%信頼区間と呼ぶ。
…………………④ を平均値の95%信頼区間と呼ぶ。
信頼度ではなく信頼係数という言い方もあります。正規分布なら上の①~④の2は1.96が正しい、などという細かいことを問題にしているわけではありません。
例題に書かれた平均値の信頼区間に関する考え方は、図に描くとイ)からロ)が導けるという論理です。
【大いなる誤解】
イ)の方は、母集団のパラメータが未知なのですから、実務的には何も教えてくれない絵空事です。問題はロ)です。ロ)の意味はある調査から求めた標本平均があって、その上下の一定幅の区間に母平均が分布するということなのでしょうか。数値例でいうとNはとても大きいとして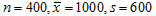 で④を適用すると、
で④を適用すると、
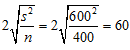
したがって母平均が次の区間に入る確率が0.95だといえるのかどうかという問題です。
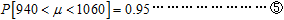
調査で問題にしている確率変数をXとして、n個のXが独立同一分布に従うと仮定しますと、n個のXの標本平均の統計量は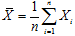 であって、それ自体が確率変数になります。ですから1回の調査から得られた平均値は母平均μなのではなくて確率変数
であって、それ自体が確率変数になります。ですから1回の調査から得られた平均値は母平均μなのではなくて確率変数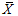 の1つの実現値
の1つの実現値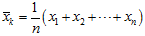 に過ぎないのです。
に過ぎないのです。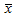 につけた下付き添字のkは第k回目の調査結果であることを表します。ですからもし第2回目の調査を行えば、n個の違ったデータが観測されるわけですから、その平均値も
につけた下付き添字のkは第k回目の調査結果であることを表します。ですからもし第2回目の調査を行えば、n個の違ったデータが観測されるわけですから、その平均値も に変わりますし、当然ながら標本分散
に変わりますし、当然ながら標本分散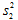 も
も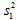 とは違った値になります。ですからロ)の区間は中心の位置だけでなく区間の幅までも調査のたびに変動するのです。次の図をご覧ください。調査回数がk=1,2,…100の場合の模式図です。
とは違った値になります。ですからロ)の区間は中心の位置だけでなく区間の幅までも調査のたびに変動するのです。次の図をご覧ください。調査回数がk=1,2,…100の場合の模式図です。
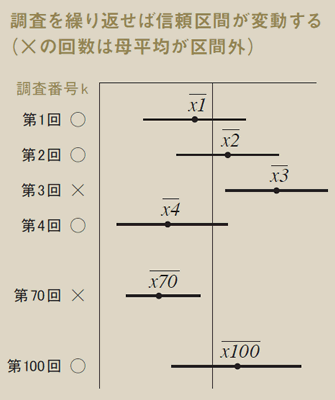
さてμは定数ですし、特定の調査から得られた⑤の区間は固定されますから、μは区間[940,1060]に入るか否か(1か0)のどちらかであって、95%の確率でこの区間に入るというような確率的な意味合いは持ちません。つまり⑤式の確率的解釈は明確な誤りです。確率変数と実現値の混同が間違ったコメントを生んだのでしょう。全く同一の調査をk=1,2,…,Kと繰り返すことは実際にはほとんどなく、たいてい調査は第1回で終わってしまいます。そのため、調査をやりなおすたびに信頼区間が変動する、という事実に出会う機会がなかったのでしょう。でも想像してみれば信頼区間が変動するのは当然だと思いませんか。
1970年~1980年代にリサーチャーが読んでいた実務書には例題と同じ誤りがよくありました。比較的よく知られた調査の実務書のどれをみてもみな同じパターンで書いてあるので、逆にさかのぼってみると1950年代に出版された統計調査の本にまでさかのぼれます。どの本が間違いの元祖かという責任追及が本コラムの目的ではありませんが、誤った理解が普及してしまったのは困ったものです。
きっと推測統計学に詳しくない読者のために、物事を分かりやすく説明しようという親切心からの記述だったのだろうと思います。「テキストを疑いながら読む」ことは学びの第1歩ですから好ましいことですが、誤解したままの人がいてもいいのか?という疑問は残ります。
4.お勧めの統計学の本
リサーチの実務マニュアルには、質問文の作り方だとかインタビューの仕方など、まさにリサーチの専門的な業務の進め方が書かれています。ですから、そうした本は必要だし価値はあるのです。しかしながら手軽なビジネス書や実務マニュアルに統計理論や数式まで任せるのが不安であれば、いっそのこと統計学の専門家が書いた専門書を読んだらどうでしょうか。
前節で指摘した問題に関しては、たとえば竹村彰通(2007)「統計第2版」協立出版の109頁では「μはパラメータの真値であり、これは固定されている。確率的に変動するのはIという区間である。つまり、区間を何度も作ると、その形の区間がμを含む割合が95%になるという意味合いである」、とちゃんと書いてあります。
このネイマン流の確率言明について、蓑谷千凰彦(2009)「これからはじめる統計学」東京図書(253頁)においても同様に、100回調査をすれば、それぞれの調査ごとに1本ずつ違った信頼区間が得られ、計100本の信頼区間のうち平均して95本がμの真の値を含むであろう、という意味の説明をしています。第1回目の調査でいきなり最終的な信頼区間が確定するわけではないし、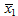 がμに一致するという根拠もないのです。
がμに一致するという根拠もないのです。
上記した2冊の本は、どちらもすっきりと分かりやすく統計学を解説されているので、初心者の方にもお勧めしたいと思います。
【略 歴】
千葉大文理学部卒業後市場調査会社に就職、埼玉大大学院修了、千葉大・筑波大講師、専修大・都立大・首都大教授を経て多摩大学大学院客員教授。学習院マネジメントスクール講師、日本マーケティング・サイエンス学会論文誌編集委員、日本行動計量学会理事。
主な著書に『アンケート調査入門』東京図書(編著)、『最新マーケティング・サイエンスの基礎』講談社、『Rによるマーケティング・シミュレーション』同友館、『入門共分散構造分析の実際』講談社、『魅力工学の実践』海文堂出版、『入門多変量解析の実際第2版』講談社、『新製品開発』朝倉書店(朝野熙彦・山中正彦著)などがある。